Reason Like a Champion
Logic and Philosophy
Some questions have answers which are easy to ascertain. Is it raining outside? Look out the window. Where is President Biden today? Check CNN. Other questions require data collection. How acidic is the water in the St. Joseph River? Better do some Ph tests. How many stars are in the Milky Way? We will probably never know, because the counting is so difficult and light only travels so fast.
Still other important questions require not only gathering observable data but also reasoning from more basic principles. Is it logically possible for God to exist and there to be pointless evils? Is it ever morally acceptable to kill someone? Is there a mathematical set that contains all and only those sets that do not have themselves as members? These are philosophical questions, and evidence for answers to philosophical questions typically requires not only beliefs about the world but also arguments. Good arguments provide reasons to believe particular theories–theism, utilitarianism, naive set composition. Of course the subject of an argument need not always be so lofty. You can argue from more basic principles that burritos are not sandwiches.
Philosophers have a well-developed system for determining whether arguments are good or bad: logic. Logic is the branch of philosophy concerned with general theories of what makes arguments good or bad, regardless of the argument’s subject matter. And logic has been the central, unifying branch of philosophy at least since Aristotle. One of our major goals for this class is to teach you how to recognize arguments and evaluate them—to give you the tools of informal logic.
How to Argue
What Arguments Are
What Arguments Are
-
The Basics
-
Premise-Conclusion Form
-
The Santa Argument
-
Santa in P-C Form

An argument is a set of sentences—called premises—that aim to support a particular conclusion. In a debate, the conclusion is called the proposition. Propositions are any claims that can be true or false. [Contrast this with questions, exclamations, or sentences that are too unclear to ever be true or false.]
For example, suppose you are wondering what Lucy’s vision is like. Peter offers you the following argument:
Every driver in Indiana has passed both an eye exam and a written licensing test. Lucy drives in Indiana. So Lucy must have passed an eye exam.
In this passage, the last sentence is the conclusion and the other two sentences are the premises. The premises give the reasons for believing the conclusion. The conclusion doesn’t always appear at the end of informal arguments. For example, you can imagine Peter giving the following reasoning:
Lucy must have passed an eye exam. After all, every driver in Indiana has passed both an eye exam and a written licensing test, right? And Lucy drives in Indiana.
This argument leads with the conclusion and then lists the premises.
In philosophical arguments, we often want to be very explicit about what the premises and conclusion are, and how the premises logically lead to the conclusion.
One way to make the argument more explicit is to put it in premise-conclusion form. To put an argument in premise-conclusion form, list each premise with a number and then put the conclusion at the end. Note that you want to state the main claim of the premise, but you don’t have to restate the sentence verbatim. Sometimes a good argument outline will just present the core claim of the premises.
Here is one way we might put the Lucy argument in premise-conclusion form:
- (1) Every driver in Indiana must pass both an eye exam and a written licensing test.
- (2) Lucy drives in Indiana.
- (C) Lucy must have passed an eye exam.
Sometimes arguments are quite complicated, and we want to explicitly discuss one of the argument’s premises. This list form makes it very clear which premise is which. For example, here is a somewhat more complicated argument (inspired by St. Anselm).
God is the being than which none greater can be conceived. Suppose God did not exist. We could conceive of a being with all of God’s properties who also exists. That being would be greater than God. But given our definition, this is impossible. Therefore God exists.
This argument requires you to make some decisions about how the premises support the conclusion. Often times charting out an argument will require you to simplify it somewhat. This also requires some critical thinking. One way to put this argument in premise-conclusion form is as follows:
- (1) Nothing greater than God can be conceived..
- (2) If God did not exist, then we could conceive of a being with all of God’s properties who also has the property of existing.
- (3) A being who exists is greater than a being who does not exist.
- (4) So if God does not exist, then there is a conceivable being greater than God (given (2) and (3)).
- (5) But according to (1) there is no conceivable being greater than God.
- (C) So God exists.
There are two nice features of having this argument in premise-conclusion form. First we can fill in a missing but intended bit of the reasoning, using premise (4) and referencing premise (1). Often arguments in English skip explicit steps, but in logic we want to make every step super clear. Second, now that all of the pieces of the argument are laid out clearly before us, we can start to decide whether the argument is any good. For example, is premise (3) true? What does “greater than” mean? We’ll settle this with even more reasoning and argument.

Let’s try a more complex example. Here is an argument from a NY Times article on whether it is appropriate to lie to your children about the existence of Santa Claus:
Parents should tell their children the truth about Santa Claus when their children signal they are ready to hear it. When are they likely to be ready?
Before the age of six, most children’s thinking will make questions and doubting about magical figures unlikely. The richly novel environment of Christmas will pique their curiosity. By the age of seven, as their thinking becomes more concrete and logical, many will wonder why there are so many Santas, how all homes can be visited in one night, or why last year’s request for a pony for the apartment was denied. Also by seven, some precocious peers or an older sibling will have (often gleefully) sown doubts.
So the key time for parents to be sensitive to signals is probably from the age of five and a half to seven. The signals are most likely to come in the form of direct questions about Santa-related inconsistencies, or more subtle comments. Children may also show less interest in seeing Santa, writing to Santa, or talking about Santa.
Try to pare the argument down to it’s key premises and conclusion. Once you’ve tried it, compare your approach with the outline on the next tab. Hint: This argument has an unstated assumption.
Here is one way to distill the argument:
- (1) Before age six, children lack concrete, logical reasoning abilities.
- (2) After age six, children have concrete, logical reasoning abilities.
- (3) It is fine to portray something fictional as real if and only if the person you are portraying it to lacks concrete, logical abilities. [Suppressed assumption].
- (C) It is fine to portray Santa as real to children under six, but you must be sensitive to when they develop concrete, logical reasoning.
Do you think (3) is correct?
Argument
Evaluating Arguments
Philosophers have precise ways of evaluating arguments. The very best sort of argument is valid, sound, and informative. Throughout this course, we will often be trying to figure out whether arguments meet any or all of these criteria. Let’s discuss each in turn.
Tools for Evaluating Arguments
Tools for Evaluating Arguments
-
Validity
-
Soundness
-
Informativeness
The first question we will ask about arguments surveyed in this class is—do the premises logically support the conclusion?
Definition of a Valid Argument: A valid argument is an argument such that it is impossible for the premises to be true and the conclusion false. Another way to put this is the premises entail the conclusion by accepted logic. Still another way to put this is if all of the premises are true, then the conclusion must be true. A final way to put the very same point: a valid argument is an argument with no possible counterexample. We won’t focus much on differences in these formulations in this class (but you would in your next logic course!)
If an argument is not valid, then it is invalid. Here are examples of some valid arguments:
- (1) All Notre Dame students are human beings.
- (2) Veronica is a Notre Dame student.
- (C) Therefore Veronica is a human being.
Here is another one:
- (1) If someone is a Notre Dame student, then they are a Cylon robot.
- (2) Veronica is a Notre Dame student.
- (C) Therefore Veronica is a Cylon robot.
The second argument is ridiculous, but it is still valid. Why? Because if the first and second premises were true (they aren’t!… I hope… but keep an eye on Veronica…) then they would force the conclusion to be true. Validity is about the structure of the argument as a whole, not the particular premises and conclusion.
Here is an example of an invalid argument:
- (1) Some Purdue students went to public high school.
- (2) Every Purdue student has taken a standardized test.
- (3) Richard is a Purdue student.
- (C) So Richard took a standardized test at a public high school.
The argument is invalid because the premises do not force the conclusion to be true. The first premise only contends that some Purdue students went to public school. It may be that Richard only went to private school. And if this is the case, all of the premises might be true, but it would still be false that Richard took a test at a public school.
To show an argument is invalid, you must give a counterexample.
Definition of a Counterexample: A counterexample to an argument is a description of a possible situation where each of the premises are true, but the conclusion is false.
In informal logic, it is usually sufficient to write out the counterexample to an argument as just a short description. For example, suppose I give you an argument like this:
- (1) If Mary is 21, then she is old enough to drive.
- (2) Mary is old enough to drive.
- (C) Mary is 21.
It is easy to think of a counterexample. Here is one:
Counterexample: Suppose Mary is 83 years old. The first premise is true, since being 21 is sufficiently old for being able to drive. The second premise is true, since an 83 year old is old enough to drive. But the conclusion is false, since Mary is not 21. Therefore the argument is invalid.
Remember this argument from earlier:
- (1) Every driver in Indiana must pass both an eye exam and a written licensing test.
- (2) Lucy drives in Indiana.
- (C) Lucy must have passed an eye exam.
On one plausible reading it is invalid. See if you can show why by providing a counterexample. [If you can’t get it right away we’ll give you the answer further down.]
It is a good thing for an argument to be valid, but as we have seen, valid arguments can have silly or otherwise false premises. Valid arguments with false premises don’t give you a particularly good reason to believe their conclusion. So the second way we evaluate arguments is with respect to the truth of their premises:
Definition of a Sound Argument: A sound argument is a valid argument whose premises are all true. If an argument is either invalid or has at least one false premise, then it is unsound.
Here is an example of a sound argument:
- (1) All living humans have chromosomes.
- (2) Anything that has chromosomes is at least partly an organic substance.
- (C) All living humans are at least partly an organic substance.
The argument is sound because (1) it is valid–it is impossible to find a situation where both premises are true and the conclusion is false, and (2) all of the premises are true, as a matter of biological fact.
Here is an example of an argument that is valid but not sound:
- (1) All humans are awake.
- (2) Anything that is awake has a neurological system.
- (C) All humans have a neurological system.
The argument is valid and the conclusion is true. But it is not sound because one premise is false–premise (1). To show the argument is unsound, we just need to find an actual example of one human who is asleep. We can also derive a more general lesson from this: sometimes invalid or unsound arguments have true conclusions. The “all humans are awake” argument has a true conclusion, but it is unsound.
Validity and soundness are very good features of an argument. But they are still not enough, because some arguments can meet these criteria but still not provide evidence for their conclusion. And the whole point of giving an argument is to support a proposition.
For example, suppose I give you the following argument for why the Earth revolves around the Sun:
- Galileo performed some experiments regarding gravity. The Earth is part of a heliocentric solar system. So the Earth revolves around the Sun.
This argument is, frankly, stupid. The second premise just repeats the conclusion using slightly different terminology. It is valid and sound, but it won’t convince anyone who doesn’t already know that the Earth revolves around the Sun. This points us to our last criterion for a good argument. Good arguments are informative.
It is somewhat more difficult to settle on a definition of informativeness. Here is how we will understand it for our purposes in this course:
- Definition of an Informative Argument: An argument is informative if it is sound and the conclusion does not appear explicitly (or close enough) as a premise. If the conclusion appears as a premise, then the argument is question-begging.
Another way of thinking of informativeness holds that nobody would believe one or more of the premises unless they already believed the conclusion.
Question-begging arguments, like the Galileo argument, just assume what they are supposed to prove. The best arguments should convince you of something you didn’t already believe using evidence you can accept.
Defining Terms-When Good Arguments Go Bad
Sometimes we can tell an argument is bad, but diagnosing what precisely has gone wrong is tricky. Fallacies are just argument forms that look like they are good—they tempt you to accept the conclusion— but really aren’t. Equivocation is one common fallacy in philosophical reasoning–a fallacy we will see in several of the arguments we consider in this course.
- Definition of Equivocation- An argument equivocates if a key term changes meaning throughout the premises, rendering the argument invalid.
For example, consider the following argument:
- (1) Man is the only rational being.
- (2) No woman is a man.
- (C) No woman is rational.
This argument is invalid. Why? (I mean superficially it looks valid.) It is invalid because we typically mean different things by the word “man”. Premise (1) only seems true if we understand “man” to mean human. Premise (2) only seems true if we mean “man” to mean biological male. So the argument equivocates on the meaning of “man”. If you just fixed on one definition, the argument would be unsound.
Worries about validity should make you very careful about defining key terms in arguments and checking to make sure that authors have defined key terms consistently and correctly.
Which brings us back to the eye exam argument:
- (1) Every driver in Indiana passed both an eye exam and a written licensing test.
- (2) Lucy drives in Indiana.
- (C) Lucy must have passed an eye exam.
In (1), it seems “driver” must be interpreted as “legal driver” to possibly be true. But in (2) “drives” could easily just mean “actually operates a car”. She might not even have a license. Equivocation! Not cool.
Why Be Good at Logic?
Why Be Good at Logic?
-
Arguments Are Everywhere
-
Professional and Financial Incentives
-
The Ultimate Aim
You are going to see arguments in major news sources, in meetings and in every other course you are taking. You will rely on arguments to make difficult decisions and to convince others of what to believe. Logic is useful because it is a skill that applies to absolutely any subject matter. Over the semester, we want you to get better at finding important arguments and stress-testing them. We also want you to discover arguments you find compelling and let them structure your thought. Moreover…
… it can be lucrative to be good at philosophical argument! Every branch of study and any career you might pursue will reward you for being able to give strong arguments and identify and repair weak ones.
Philosophy majors typically top MCAT, LSAT, GMAT score charts, in part because logical skill is key to these professions. But it’s not just about career success…
More on the instrumental value of studying philosophy here.
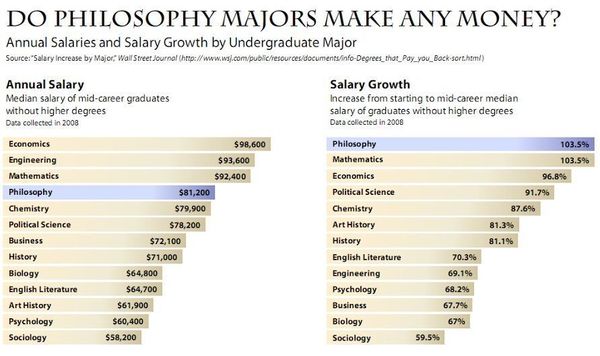
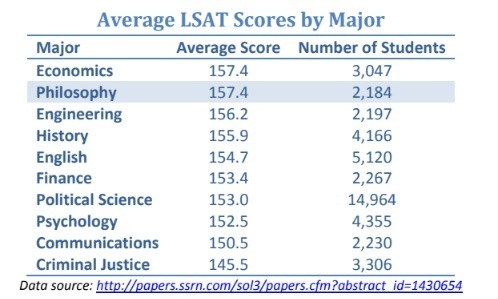
… really we develop these skills so we can flourish. Knowing the truth about even very abstract subjects gives our lives meaning and value. And to know the answers to our most important philosophical questions, we must rely on good arguments. As Aristotle puts it:
If happiness is activity in accordance with virtue, it is reasonable that it should be in accordance with the highest virtue; and this will be that of the best thing in us. Whether it be reason or something else that is this element which is thought to be our natural ruler and guide and to take thought of things noble and divine, whether it be itself also divine or only the most divine element in us, the activity of this in accordance with its proper virtue will be perfect happiness. This activity…[consists in] contemplating truth.
Nicomachean Ethics, Chapter 7
Wherever the argument, like a wind, tends… there must we go.
-Plato, Book III of The Republic
Acknowledgments
This digital essay was prepared by Paul Blaschko and Meghan Sullivan.























